線性回歸

談到機器學習的演算法，首先我們從最簡單的方法談起。相信如果各位有稍微接觸過統計學這門學科的話，一定不會對我們今天要介紹的主角**線性回歸(Linear Regression)**感到陌生，其最簡單的形式為一條描述一個X變數(特徵)與一個Y變數(目標)之間關係的直線(見圖1)，且是用來解決機器學習當中的回歸問題。

當我們的機器學習問題當中包含了兩個或以上的特徵時，線性回歸的形式就不會再是一條直線了，而是會隨著我們的特徵數目多寡，以平面、三維空間甚至是更高維度的空間出現，而其數學式子可以使用如圖2的形式來表達，其中的W表示為對應X(特徵)之權重，可以理解為當該X變動一單位時，對預測目標值Y的影響程度。因此線性回歸預測值的產生就是將各特徵值以對應的權重加權後，再進行加總而得。

那到底我們要怎麼從手上的資料，來建構出線性回歸模型呢? 在這裡介紹兩種方式，首先是第一種矩陣運算的方式(見圖3)，我們可以透過以Y與X進行的矩陣運算來得到X對應的權種值，以建構線性回歸模型，但是這種方式在處理較大型的資料上會較不實用。而另一種方式就是機器學習中較常見的方式，也就是以 梯度下降(Gradient Descent) 的優化過程來進行的，從最初的隨機賦予權重開始，不斷地計算目前預測值和真實目標值之間的差異，接著以梯度下降計算權重在迭代後應該更新的方向與大小，持續調整權重值至最理想的狀態，關於梯度下降的作法，會在後面的文章較詳細地和各位說明。

線性回歸模型較適合用來處理當目標值與特徵之間的關係為線性的情況，因此比如說當一目標值隨著特徵值從小到大的變化會出現時大時小的變化趨勢時，就比較不適合，在這種情況下，可能就要考慮使用較為複雜的模型。而線性模型可以透過加入 正則化(Regularization) 的元素，產生如 Lasso Regression 或者 Ridge Regression等變形，有機會可以在處理機器學習 泛化(Generalization) 上取得更好的表現。

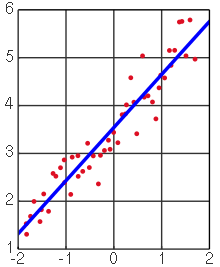
圖1
Source: https://zh.wikipedia.org/wiki/線性回歸

圖2
Source: Coursera - Launching into Machine Learning

圖3
Source: Coursera - Launching into Machine Learning